-
Comprender el significado físico de momento lineal o cantidad de movimiento como medida de la capacidad de un cuerpo de actuar sobre otros en choques. (movimientos unidimensionales)
-
Comprender la relación entre impulso (de una fuerza constante) y momento lineal, así como el principio de conservación del momento lineal de un sistema en ausencia de impulso externo.
-
Comprender la noción de choque elástico e inelástico.
-
Aplicar la conservación del momento lineal al cálculo de velocidades o masas de partículas que chocan entre sí en choques elásticos e inelásticos unidimensionales.
-
Comprender cualitativamente los cambios de dirección que se producen en choques no frontales.
-
Aplicar la conservación del momento lineal al cálculo de velocidades o masas de partículas en el caso de desintegración de un cuerpo en fragmentos (sólo en dos o tres fragmentos)
viernes, 23 de julio de 2010
conclusiones
ejemplos
CONSERVACIÓN
DE LA CANTIDAD DE MOVIMIENTO (masa variable)
3.3.31.* Un contenedor impermeable, abierto
por la parte superior con una capacidad tal que su masa lleno de agua es el
doble que cuando está vacío, m0 y se dispone sobre una plataforma
móvil que rueda sin rozamiento por una vía rectilínea a una velocidad
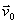m/s. Comienza a llover de forma que el ritmo
con que se llena el contenedor es de
n kg/s. En esta situación podrás afirmar que:
m/s. Comienza a llover de forma que el ritmo
con que se llena el contenedor es de
n kg/s. En esta situación podrás afirmar que:
a)
EL CONTENEDOR MANTIENE SIEMPRE LA MISMA VELOCIDAD
b)
EL CONTENEDOR ADQUIERE UN MOVIMIENTO UNIFORMEMENTE RETARDADO
c)
EL CONTENEDOR TERMINARÁ DETENIÉNDOSE
d)
LA MÍNIMA VELOCIDAD ALCANZADA POR EL
CONTENEDOR ES
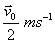
e)
EL RECORRIDO EFECTUADO POR EL CONTENEDOR HASTA LLENARSE ES DE
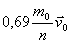
3.3.32. Si el contenedor anterior fuera
arrastrado por una locomotora, por los raíles con los que el coeficiente de
rozamiento es
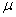, para que mantuviera durante el tiempo de llenado por la lluvia una velocidad
constante
, la locomotora tendría
que aplicar una fuerza horizontal sobre el contenedor y la potencia desarrollada por esa fuerza cuando
la de rozamiento es máxima, vale, expresada en vatios:
, para que mantuviera durante el tiempo de llenado por la lluvia una velocidad
constante
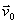, la locomotora tendría
que aplicar una fuerza horizontal sobre el contenedor y la potencia desarrollada por esa fuerza cuando
la de rozamiento es máxima, vale, expresada en vatios:
a) v0(
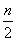v0 + 2
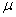m0g)
v0 + 2
m0g)
b) v0(nv0 - 2
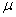m0g)
m0g)
c) v0(
m0g - nv0)
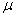m0g - nv0)
d) v0²(n
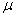m0g)
m0g)
3.3.33. Los camiones de riego que en las
madrugadas suelen limpiar nuestras calles, son un claro ejemplo de un sistema
que debe procurar mantener una velocidad constante pese a la pérdida continua
de masa. Si un camión cisterna, tiene una masa m, cuando está completamente
cargado, y va lanzando un chorro de agua con velocidad
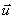respecto del camión, en sentido contrario
al de su marcha, siendo el régimen de gasto de agua n kg/s. La potencia disipada
en vatios para lograr que el camión
mantenga su velocidad constante es:
respecto del camión, en sentido contrario
al de su marcha, siendo el régimen de gasto de agua n kg/s. La potencia disipada
en vatios para lograr que el camión
mantenga su velocidad constante es:
a) unv b) u²n/v c) - nv²/u
d) - uvn e) NADA DE LO DICHO
3.3.34. Los núcleos atómicos inestables
(fuera de la franja de estabilidad), se desintegran espontáneamente emitiendo
partículas que salen a gran velocidad, lo cual deberá provocar una gran variación
de la cantidad de movimiento del núcleo inicial. Si uno de masa m, lanza una
partícula de masa cinco veces menor, con una velocidad
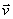, el residual se desplazará
con velocidad:
, el residual se desplazará
con velocidad:
a)
5
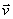b) -5
b) -5
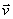
c)
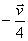d)
d)
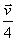
3.3.35.* Imaginemos que un camión aljibe,
con un peso bruto de 12 t, y una tara de 6000 kg , sólo se moviera, por efecto de la salida
del agua de riego, con un ritmo continuo de 20 litros por minuto, y una velocidad
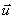de 1m/s respecto del camión. Si inicialmente
antes de comenzar a regar su velocidad era de 10 km/h , dirás que:
de 1m/s respecto del camión. Si inicialmente
antes de comenzar a regar su velocidad era de
a)
SÓLO PODRÁ REGAR DURANTE 5 HORAS
b)
SU VELOCIDAD MÁXIMA FUE DE 12,5 km/h.
c)
SU ACELERACIÓN MEDIA FUE DE 0,2 m/s².
d)
AL CABO DE 2 HORAS SU VELOCIDAD SERÍA DE 10,8
km/h.
3.3.36.* El movimiento de los cohetes interplanetarios
se basa en el efecto de la propulsión a chorro, aplicado a los motores de
avión a partir de 1941, esto es los gases producidos en la combustión de del
propelente, las tres cuartas partes de la masa total m0, salen
con una velocidad u respecto a la del cohete, con lo cual éste va incrementando
su velocidad. Si la masa antes de la
expulsión de gases a un ritmo de n kg/s, es m0, podrás decir que
en el campo gravitatorio terrestre (suponiendo las variaciones de g =9,8 m/s², despreciables) así
como la resistencia del aire
a) EL MOVIMIENTO QUE REALIZA EL COHETE INICIALMENTE
ES UNIFORMEMENTE RETARDADO
b)
SÓLO EL MOVIMIENTO SERÁ UNIFORMEMENTE RETARDADO AL CABO DE UN TIEMPO t= 3m0/4n
c) EL COHETE TIENE SU VELOCIDAD MÁXIMA AL SALIR
d) LA MÁXIMA VELOCIDAD ES 1,39
.
.
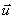3.3.37. Los cohetes interplanetarios, van
quemando combustible, frecuentemente oxígeno e hidrógeno líquido, que produce
unos gases que salen con una velocidad constante
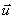, respecto a la del cohete
y por lo tanto su masa disminuirá. En ausencia de interacciones gravitatorias,
cuando su masa sea la cuarta parte de la inicial, la velocidad del cohete
será en valor modular respecto a la de los gases expulsados un número de veces
igual a :
, respecto a la del cohete
y por lo tanto su masa disminuirá. En ausencia de interacciones gravitatorias,
cuando su masa sea la cuarta parte de la inicial, la velocidad del cohete
será en valor modular respecto a la de los gases expulsados un número de veces
igual a :
a) 1 b)
1,38 c) 0,69
d) 0,1 e)
NADA DE LO DICHO
3.3.38. Cuando la velocidad de un cohete
interplanetario fuera de un campo gravitatorio respecto a un observador inercial
es igual a la de salida de sus gases, su masa se habrá reducido a:
a)
LA MITAD b) LA CUARTA PARTE
c)
TRES CUARTAS PARTES d) POCO MAS DE UN TERCIO
e)
NADA DE LO DICHO
3.3.39. Hace algún tiempo hemos observado
por la televisión el lanzamiento del primer satélite espacial español, el
Hispasat. Al principio parecía que iba muy lento, y después aumentaba su velocidad
hasta desaparecer. Si consideramos que el cohete con satélite y combustible
tiene una masa inicial de 100t, que las tres cuartas partes de aquella, corresponden
al combustible y que su combustión produce unos gases que salen expulsados
con una velocidad de 4.000 m/s, respecto al cohete, siendo el gasto de combustible
10000 kg/s, podrás asegurar, por lo tanto, si g=9,8 m/s², y despreciamos la resistencia
del aire que:
a)
LA MÁXIMA VELOCIDAD ALCANZADA SERÍA 5472 m/s.
b)
AL CABO DE 1s, SU VELOCIDAD ERA TAN SOLO DE 412 m/s.
c)
EL TIEMPO DE COMBUSTIÓN DE LOS GASES FUE DE 7,5s.
d)
LA MITAD DE LA VELOCIDAD MÁXIMA
e)LA
ACELERACIÓN DEL HISPASAT, MIENTRAS QUEMA COMBUSTIBLE, ES DIRECTAMENTE PROPORCIONAL
AL TIEMPO.colision y tipos
COLISIONES
En un choque
2 objetos se aproximan uno al otro, interaccionan fuertemente y se separan.
Antes de la colisión, cuando están alejados, los objetos se mueven con
velocidades constante. Después del choque se mueven con velocidad constante,
pero distintas. Normalmente interesa conocer las velocidades finales de los
objetos cuando sus velocidades iniciales y las características del choque son
conocidas.
En el mundo de las
colisiones, podemos encontrarlas diferenciadas de 2 formas , las
cuales se denominan, colisiones elásticas e inelásticas.
COLISIÓN INELÁSTICA
Se llama a la
colisión en la cual se pierde
Energía Cinética
. Bajo ciertas condiciones especiales,
se pierde poca energía en la colisión.
COLISIÓN ELÁSTICA
Es el caso
ideal, cuando no se pierde
Energía Cinética
,
un ejemplo es la pelota de caucho endurecido
que cae sobre algo duro y macizo, en un piso de mármol, por ejemplo,
y rebota aproximadamente hasta la misma altura de su punto de
partida, siendo despreciable la energía perdida en su choque contra
el piso.
EJEMPLO
Un camión de
carga de 30,000 kg que viaja a 10.0 m/s choca contra un automóvil de
1700 kg que viaja a 25 m/s en dirección opuesta .Si quedan unidos
después del choque, ¿a qué rapidez y en qué dirección se moverán?
Razonamiento : Llamando x a la dirección positiva, se aplica la conservación de la cantidad de movimiento (obviamente que la EC se conserva en este choque). Hagamos que ν sea su rapidez combinada después de la colisión.
Razonamiento : Llamando x a la dirección positiva, se aplica la conservación de la cantidad de movimiento (obviamente que la EC se conserva en este choque). Hagamos que ν sea su rapidez combinada después de la colisión.
Cantidad de
movimiento antes = cantidad de movimiento después.
Nótese que la
velocidad del automóvil es negativa. Resolviendo para
ν
da,
ν=8.l
m/s. El signo positivo para
ν
indica que el movimiento final es en la dirección positiva x, o lo
que es lo mismo, en la dirección en la cual se movía el camión de
carga.
Nótese que el camión de carga se frenó sólo ligeramente, mientras que la dirección del movimiento del automóvil se invirtió. Conviene estimar la fuerza media sobre el conductor del automóvil durante la colisión, pero se deja como ejercicio. (Si el cibernauta desea hacer esta estimación, tome en cuenta que el impulso que se ejerce sobre el conductor es igual al cambio en la cantidad de movimiento del conductor.
Nótese que el camión de carga se frenó sólo ligeramente, mientras que la dirección del movimiento del automóvil se invirtió. Conviene estimar la fuerza media sobre el conductor del automóvil durante la colisión, pero se deja como ejercicio. (Si el cibernauta desea hacer esta estimación, tome en cuenta que el impulso que se ejerce sobre el conductor es igual al cambio en la cantidad de movimiento del conductor.
Colisiones
Frontales
Observe
en el siguiente applet , en el cual se lograra realizar las siguientes
actividades.
Se
podra tomar como variable, las diferentes velocidades de los cuerpos,
generando así una colisión.
Variando
el coeficiente de restitución , se lograra observar en que consiste dicho
coeficiente
y por
ultimo se introducirá una variable, que es la relación de masas que se
encontraran en la colisión.
COMPONENTES DE LA CANTIDAD
DE MOVIMIENTO
Dado que la cantidad de
movimiento es un vector , se puede hablar de sus componentes. Por ejemplo, el
objeto que se muestra en la figura, tiene una cantidad de movimiento P.
Pero el vector cantidad de movimiento se compone de tres
componentes designadas por Px
,Py,Pz, y el
vector de suma de estas componentes es equivalente al vector original
P.
Similarmente, si un sistema de objetos tiene una cantidad de movimiento total
P
, entonces la cantidad de movimiento total se puede
reemplazar por sus componentes. si se aísla el sistema, la ley de conservación
de la cantidad de movimiento indica que no habrá ningún cambio ni en la cantidad
de movimiento total ni en sus componentes. Por consiguiente, se puede establecer
que las componentes de la cantidad de
movimiento total se conservan para un sistema aislado.
EJEMPLO :
Una pelota se mueve a
5.0 m/s choca contra una pelota igual de masa que esta en reposo, como se
muestra en la figura. Después de la colisión, una de las tres pelotas tiene la
velocidad mostrada en la figura . ¿Cuales son las componentes de la velocidad
para las otras 2 pelotas después de la colisión?
ANTES
DESPUÉS
RAZONAMIENTO:
Se sabe que la pelota también se moverá en el plano XY.
Escribiendo la conservación de la cantidad del movimiento lineal para las
coordenadas X y Y, tenemos:
COORDENADA X:
m.(5m/s) + 0 =
m.(2m/s).cos50º + mvx
COORDENADA Y:
0 + 0=m(2sen50º) + mvy
La
primera ecuación da vx=3.7
m/s , mientras que la segunda da vy=-1.53
m/s . De esta ecuación se puede ver que la segunda
pelota se mueve describiendo un ángulo theta bajo el eje +x donde:
Tan θ = 1.53/3.7 = 22º
La
magnitud de su velocidad es :
El péndulo balístico se
usa para determinar la velocidad de una bala midiendo el ángulo que gira un
péndulo después de que la bala se ha incrustado en él. El péndulo balístico
consta de un bloque suspendido de una cuerda, que suponemos inextensible y sin
peso.
Si un cuerpo de masa
m y velocidad
u se
mueve a lo largo de la horizontal (o muy aproximadamente) y choca frontalmente
contra otro de masa M inicialmente en reposo y queda incrustado en él ocurre un
choque plástico) el conjunto empieza a moverse con una velocidad
.
.
La fuerza externa que actúa sobre el sistema es
la fuerza constante de gravedad, cuya acción en nuestro caso, durante el tiempo
que actúan las intensas fuerzas impulsivas internas, es insignificante; con lo
que podemos suponer que éste choque plástico ocurre sin la acción de fuerzas
externas. En este caso sabemos que se conserva la cantidad de movimiento lineal
de todo el sistema. Luego, esta magnitud antes del choque P1=mu (recuerde que el cuerpo de masa M está inicialmente en reposo) será igual a
la cantidad de movimiento lineal después del choque P2=(m+M)V,
es decir:
Mu=(m+M)V
(1)
de
donde
V=m/(m+M)u (2)
Esta expresión nos dice que ahora el cuerpo de
masa (m + M) se empezará a mover en la misma dirección y sentido en que se movía
el cuerpo de masa m. Esto nos permite rescribir la fórmula (2) con los módulos
de las velocidades:
(3)
Expresión que nos indica
que el módulo de la velocidad V inmediatamente después del choque
(simplemente
la velocidad en lo que sigue) será siempre menor que la velocidad u, y
será
cuanto menor, cuanto mayor sea
M.
Si ahora el cuerpo M
cuelga de un hilo largo (ver figura 2), supuesto sin masa e inextensible, fijo
al punto O, el sistema empezará a moverse a lo largo de una trayectoria
circular con centro en O, bajo la acción de la fuerza de gravedad, que es
una fuerza conservativa y la tensión del hilo que no realiza trabajo en este
movimiento por mantenerse siempre perpendicular a su trayectoria.
Con lo dicho, es claro,
si despreciamos la fricción con el aire, que debe conservarse la energía
mecánica durante esta etapa del movimiento. Luego, toda la energía cinética al
inicio de la trayectoria circular se convierte en energía potencial al final de
la misma cuando la velocidad es cero. Así tomando como referencia para la
energía potencial gravitatoria la dirección a lo largo de la cual se movía el
cuerpo de masa m y se encontraba el centro de masa del cuerpo de masa M (choque
frontal) y además no tenemos en cuenta la energía cinética de rotación, podemos
escribir que:
(4)
en
donde H es la altura máxima que alcanza el centro de masas del sistema en su
movimiento circular y g la aceleración de la gravedad. Simplificando y
despejando la velocidad V del sistema, justo después del choque, nos queda:
(5)
Si ahora llamamos L a la
distancia que hay desde el punto O al centro de masas del sistema de masa
(m+M) y x al desplazamiento lateral, por consideraciones geométricas en la
figura No. 2, podemos escribir que:
(6)
y tomando además 2L >> H podemos con mucha aproximación escribir:
(6a)
De donde, despejando H:
(7)
Sustituyendo (7) en (5)
obtenemos:
(8)
Fórmula que nos permite
relacionar la velocidad V con el desplazamiento lateral x. Luego,
si realizamos el experimento descrito anteriormente de manera que se cumplan las
aproximaciones indicadas, una medida del desplazamiento lateral x nos permitiría
conocer la velocidad V del sistema después del choque y que a su vez mediante la
conservación de la cantidad de movimiento lineal en el choque plástico nos
permitiría a través de la fórmula (3) calcular el valor de la velocidad u del
cuerpo de masa m antes del choque utilizando la fórmula:
(9)
choques y colision!
Choques o colisiones
Las manifestaciones de la conservación de cantidad de movimiento son más claras en el estudio de choques dentro de un sistema aislado de cuerpos. Se dice que el sistema es aislado, cuando no actúan fuerzas externas sobre ninguna de sus partes. Las leyes que describen las colisiones fueron formuladas por John Wallis, Christopher Wren y Christian Huygens, en 1668.
Cuando dos objetos realizan una colisión, entre dichos objetos se producen fuerzas recíprocas de interacción y se dice que los objetos constituyen un sistema físico. Por otra parte, si las únicas fuerzas que intervienen son las fuerzas recíprocas se dice que el sistema está aislado.
Sobre la superficie terrestre no es posible obtener un sistema completamente aislado, pues todos los objetos están sometidos a fuerzas exteriores, tales como la fuerza de fricción o la fuerza de gravedad. Sin embargo se admiten como sistemas aislados los que están formados por objetos que se mueven horizontalmente sobre colchones de aire, capas de gas o superficies de hielo pues en estos casos el roce es mínimo y la fuerza resultante que actúa sobre los objetos que constituyen el sistema es nulo.
También se consideran como sistemas aislados aquellos casos en que las fuerzas exteriores son despreciables comparadas con la fuerza de interacción, como ocurren con bolas de billar, discos de plástico, esferas de acero, etc., que se mueven sobre superficies horizontales lisas.
Se llama choques a la interacción de dos (o más) cuerpos mediante una fuerza impulsiva. Si m1 y m2 son las masas de los cuerpos, entonces la conservación de la cantidad de movimiento establece que: m1. + m2. = m1. + m2
Donde , , , son las velocidades iniciales y finales de las masas m1 y m2.
Características en los choques
1) Los dos cuerpos pueden desintegrarse en pedazos
2) Puede haber una transferencia de masa
3) Las dos masas se pueden unir para formar una sola
4) Las masas pueden permanecer invariables. Aun en este caso hay diversas posibilidades. Los cuerpos pueden permanecer completamente inalterados, como cuando chocan dos bolas de billar, o bien se pueden deformar, como cuando chocan dos automóviles.
Choques entre dos cuerpos
Los dos son libres antes de la colisión, y puede caracterizarse, cada uno, por su cantidad de movimiento constante. Durante la interacción breve, sus cantidades de movimiento cambian, porque cada uno siente una fuerza de impulsión debida al otro. Los impulsos que sienten los dos cuerpos son iguales y opuestos, porque las fuerzas son iguales y opuestas. La ganancia de cantidad de movimiento de un cuerpo es igual a la pérdida de cantidad de movimiento del otro.
Después del choque, los dos cuerpos también quedan libres, pero tienen cantidades de movimiento distintas. Sin embargo la suma de las cantidades de movimiento no cambia.
Nótese que no todas las colisiones se describen en forma adecuada sólo con el impulso. A un cometa que entra al sistema solar y da una vuelta a causa del campo gravitacional del Sol, también se le puede considerar como que �chocó� con el Sol. El movimiento del cometa no se puede determinar mediante un breve impulso y el principio de conservación de cantidad de movimiento.
El momento total de un sistema de cuerpos que chocan no cambia antes, durante, ni después del choque. Esto se debe a que las fuerzas que actúan durante el choque son internas �fuerzas que actúan y reaccionan dentro del propio sistema-. Hay sólo una redistribución o compartimiento del momento que existía antes del choque.
Clasificación de las colisiones
En una sola dimensión.
Dos objetos físicos realizan una colisión en una dimensión, también llamada colisión frontal , cuando antes y después de la interacción el movimiento de dichos objetos se realiza a lo largo de una recta.
Si dos objetos constituyen un sistema aislado y realizan una colisión frontal, los cambios en las cantidades de movimiento de dichos objetos son iguales en módulo, pero de sentido opuesto.
= -
Si dos objetos constituyen un sistema aislado y realizan una colisión frontal, la cantidad total de movimiento antes y después de la colisión es la misma. (Ley de la conservación de la cantidad de movimiento)
Colisiones Elásticas
Cuando una bola de billar en movimiento choca de frente con otra en reposo, la móvil queda en reposo y la otra se mueve con la rapidez que tenía la primera. los objetos chocan rebotando sin deformación permanente y sin generación de calor. Cualesquiera que sean los movimientos iniciales, sus movimientos después del rebote son tales que tienen el mismo momento total. En un choque elástico en una dimensión, las velocidades relativas de las dos partículas son constantes.
Rebote
Cuando hay rebote se produce una consecuencia interesante de la conservación del momento. Considere una bola de golf que choca con una bola de boliche que se encuentra en reposo. Si el choque es perfectamente elástico, tal manera que la pelota de golf rebote con sólo una pequeñísima pérdida de rapidez, la bola de boliche retrocede con casi el doble del momento que la pelota de golf incidente. Esto es congruente con la ley de la conservación del momento, porque si el momento inicial de la pelota de golf es positivo, entonces, después del rebote, es negativo.
El momento negativo de la pelota de golf es compensado por el mayor momento de la bola de boliche. El momento neto antes y después del choque es el mismo.
Colisiones Perfectamente inelásticas
Cuando los objetos permanecen juntos después de la colisión. Los cuerpos coalecen (�se pegan�) al chocar. En tal caso, la energía mecánica no se conserva, porque no hay fuerzas externas que actúen sobre el sistema de dos partículas. Las velocidades finales son iguales ( = ). Considérese el caso de un carro de carga que viaja sobre una vía y choca con otro en reposo. Si ambos carros tienen la misma masa y se unen al chocar, ¿Es posible predecir la velocidad que tendrán unidos después del impacto? En cualquier choque, es posible decir que:
Momento total antes del choque = Momento total después del choque
Esto es cierto incluso cuando los objetos en colisión se unen o traban durante el choque. Supóngase que el carro en movimiento se desplaza a 10 metros por segundo y sea m la masa de cada carro. Entonces por la conservación del momento.
( mtotal)antes = ( mtotal)después
( m= 10)antes = (2 m x ? ) después
Puesto que después del choque se está moviendo el doble de masa, la velocidad debe ser la mitad de la que exista antes del choque, o sea 5 m/seg. Así serán iguales ambos miembros de la ecuación. Nótese la importancia de la dirección en estos casos. El momento como la fuerza son cantidades vectoriales.
Colisiones en dos dimensiones
Dos objetos realizan una colisión de dos dimensiones o bidimensional, cuando antes y después de la colisión los objetos tienen libertad de moverse en un plano, según direcciones diferentes. Experimentalmente puede comprobarse que la ley de conservación de la cantidad de movimiento es válida también para choques bidimensionales. En este tipo de choques las velocidades inicial y final no están en una sola recta. Las cantidades iniciales de movimiento de las partículas en la colisión se pueden descomponer en dos componentes mutuamente perpendiculares, y Los componentes totales x e y deben satisfacer por separado la condición de conservación.
El momento neto antes y después de cualquier choque permanece inalterable, inclusive cuando los objetos que chocan se muevan con ciertos ángulos entre ellos. Para expresar el momento neto al considerar diferentes direcciones, se requiere una técnica denominada adición vectorial.
El momento de cada objeto se expresa como un vector; el momento neto se encuentra combinando los vectores en forma geométrica. Una bomba que durante su caída explota en dos fragmentos. Los valores de momento de los fragmentos se combinan por adición vectorial para igualar el momento original de la bomba en caída.
Se pueden aplicar los argumentos de la conservación de la cantidad de movimiento a situaciones en las cuales no es cero, pero uno o dos de sus componentes sí. En estos casos, se conservan los componentes correspondientes de . El problema de un proyectil que explota en vuelo es un ejemplo en el cual se puede seguir este camino. La fuerza sobre el sistema no es cero, porque el sistema está sujeto a la gravedad. Sin embargo, esta fuerza no tiene componentes horizontales, y por tanto se conservan los componentes horizontales de . Se presentan estos casos más complicados no como un tema de estudio más profundo sino para conocer situaciones más generales y apreciar que aun cuando la idea de la conservación del momento es elegantemente simple, su aplicación a choques más complicados puede ser difícil especialmente si no se domina la adición vectorial.
Cualquiera que sea la naturaleza de un choque o por muy complicado que se presente, el momento total antes, durante y después de él se mantiene inalterable. Este concepto extremadamente útil permite aprender mucho de los choques haciendo caso omiso de la forma de las fuerzas que interactúan en ellos.
Centro de masas
Suponga que tiene dos bloques de masas m1 y m2 que están unidos por medio de un resorte comprimido. Si dichas masas son dejadas libres y se supone que no hay roce, el cuerpo de masa m1adquiere una velocidad y el cuerpo de masa m2 adquiere una velocidad , quedando luego el resorte en reposo.
La cantidad de movimiento antes de la interacción es nula porque las masas están en reposo. La suma de las cantidades de movimiento después de la interacción será: m1 + m2
Por el principio de la conservación de la cantidad de movimiento, m1 + m2= 0 Luego m1= -m2
Si la acción del resorte es instantánea, las dos masas se mueven distancias x1 y x2 de su posición inicial, con velocidades constantes, dada cada una en módulo por:
= x1 /
= x2/
Sustituyendo (2) en (1) se tiene que m1. x1/ = m2. x2/
Donde m1. x1= m2. x2
luego
Como puede notarse, esta expresión dice que las distancias recorridas por los cuerpos en relación con el punto donde partieron son inversamente proporcionales a las masas. Esto significa que la mayor distancia la recorre el cuerpo de menor masa.
El centro de masas es el punto que divide la distancia que separa los cuerpos en proporción inversa a sus masas.
Expresión matemática del centro de masa de un sistema en relación a un punto de origen.
Considere dos masas m1 y m2, cuyas distancias a un origen 0 , son respectivamente x1 y x2.
Sea c un punto llamado centro de masas del sistema, el cual está a una distancia xcm del origen.
La expresión para la coordenada x del centro de masas es:
Las manifestaciones de la conservación de cantidad de movimiento son más claras en el estudio de choques dentro de un sistema aislado de cuerpos. Se dice que el sistema es aislado, cuando no actúan fuerzas externas sobre ninguna de sus partes. Las leyes que describen las colisiones fueron formuladas por John Wallis, Christopher Wren y Christian Huygens, en 1668.
Cuando dos objetos realizan una colisión, entre dichos objetos se producen fuerzas recíprocas de interacción y se dice que los objetos constituyen un sistema físico. Por otra parte, si las únicas fuerzas que intervienen son las fuerzas recíprocas se dice que el sistema está aislado.
Sobre la superficie terrestre no es posible obtener un sistema completamente aislado, pues todos los objetos están sometidos a fuerzas exteriores, tales como la fuerza de fricción o la fuerza de gravedad. Sin embargo se admiten como sistemas aislados los que están formados por objetos que se mueven horizontalmente sobre colchones de aire, capas de gas o superficies de hielo pues en estos casos el roce es mínimo y la fuerza resultante que actúa sobre los objetos que constituyen el sistema es nulo.
También se consideran como sistemas aislados aquellos casos en que las fuerzas exteriores son despreciables comparadas con la fuerza de interacción, como ocurren con bolas de billar, discos de plástico, esferas de acero, etc., que se mueven sobre superficies horizontales lisas.
Se llama choques a la interacción de dos (o más) cuerpos mediante una fuerza impulsiva. Si m1 y m2 son las masas de los cuerpos, entonces la conservación de la cantidad de movimiento establece que: m1. + m2. = m1. + m2
Donde , , , son las velocidades iniciales y finales de las masas m1 y m2.
Características en los choques
1) Los dos cuerpos pueden desintegrarse en pedazos
2) Puede haber una transferencia de masa
3) Las dos masas se pueden unir para formar una sola
4) Las masas pueden permanecer invariables. Aun en este caso hay diversas posibilidades. Los cuerpos pueden permanecer completamente inalterados, como cuando chocan dos bolas de billar, o bien se pueden deformar, como cuando chocan dos automóviles.
Choques entre dos cuerpos
Los dos son libres antes de la colisión, y puede caracterizarse, cada uno, por su cantidad de movimiento constante. Durante la interacción breve, sus cantidades de movimiento cambian, porque cada uno siente una fuerza de impulsión debida al otro. Los impulsos que sienten los dos cuerpos son iguales y opuestos, porque las fuerzas son iguales y opuestas. La ganancia de cantidad de movimiento de un cuerpo es igual a la pérdida de cantidad de movimiento del otro.
Después del choque, los dos cuerpos también quedan libres, pero tienen cantidades de movimiento distintas. Sin embargo la suma de las cantidades de movimiento no cambia.
Nótese que no todas las colisiones se describen en forma adecuada sólo con el impulso. A un cometa que entra al sistema solar y da una vuelta a causa del campo gravitacional del Sol, también se le puede considerar como que �chocó� con el Sol. El movimiento del cometa no se puede determinar mediante un breve impulso y el principio de conservación de cantidad de movimiento.
El momento total de un sistema de cuerpos que chocan no cambia antes, durante, ni después del choque. Esto se debe a que las fuerzas que actúan durante el choque son internas �fuerzas que actúan y reaccionan dentro del propio sistema-. Hay sólo una redistribución o compartimiento del momento que existía antes del choque.
Clasificación de las colisiones
En una sola dimensión.
Dos objetos físicos realizan una colisión en una dimensión, también llamada colisión frontal , cuando antes y después de la interacción el movimiento de dichos objetos se realiza a lo largo de una recta.
Si dos objetos constituyen un sistema aislado y realizan una colisión frontal, los cambios en las cantidades de movimiento de dichos objetos son iguales en módulo, pero de sentido opuesto.
= -
Si dos objetos constituyen un sistema aislado y realizan una colisión frontal, la cantidad total de movimiento antes y después de la colisión es la misma. (Ley de la conservación de la cantidad de movimiento)
Colisiones Elásticas
Cuando una bola de billar en movimiento choca de frente con otra en reposo, la móvil queda en reposo y la otra se mueve con la rapidez que tenía la primera. los objetos chocan rebotando sin deformación permanente y sin generación de calor. Cualesquiera que sean los movimientos iniciales, sus movimientos después del rebote son tales que tienen el mismo momento total. En un choque elástico en una dimensión, las velocidades relativas de las dos partículas son constantes.
Rebote
Cuando hay rebote se produce una consecuencia interesante de la conservación del momento. Considere una bola de golf que choca con una bola de boliche que se encuentra en reposo. Si el choque es perfectamente elástico, tal manera que la pelota de golf rebote con sólo una pequeñísima pérdida de rapidez, la bola de boliche retrocede con casi el doble del momento que la pelota de golf incidente. Esto es congruente con la ley de la conservación del momento, porque si el momento inicial de la pelota de golf es positivo, entonces, después del rebote, es negativo.
El momento negativo de la pelota de golf es compensado por el mayor momento de la bola de boliche. El momento neto antes y después del choque es el mismo.
Colisiones Perfectamente inelásticas
Cuando los objetos permanecen juntos después de la colisión. Los cuerpos coalecen (�se pegan�) al chocar. En tal caso, la energía mecánica no se conserva, porque no hay fuerzas externas que actúen sobre el sistema de dos partículas. Las velocidades finales son iguales ( = ). Considérese el caso de un carro de carga que viaja sobre una vía y choca con otro en reposo. Si ambos carros tienen la misma masa y se unen al chocar, ¿Es posible predecir la velocidad que tendrán unidos después del impacto? En cualquier choque, es posible decir que:
Momento total antes del choque = Momento total después del choque
Esto es cierto incluso cuando los objetos en colisión se unen o traban durante el choque. Supóngase que el carro en movimiento se desplaza a 10 metros por segundo y sea m la masa de cada carro. Entonces por la conservación del momento.
( mtotal)antes = ( mtotal)después
( m= 10)antes = (2 m x ? ) después
Puesto que después del choque se está moviendo el doble de masa, la velocidad debe ser la mitad de la que exista antes del choque, o sea 5 m/seg. Así serán iguales ambos miembros de la ecuación. Nótese la importancia de la dirección en estos casos. El momento como la fuerza son cantidades vectoriales.
Colisiones en dos dimensiones
Dos objetos realizan una colisión de dos dimensiones o bidimensional, cuando antes y después de la colisión los objetos tienen libertad de moverse en un plano, según direcciones diferentes. Experimentalmente puede comprobarse que la ley de conservación de la cantidad de movimiento es válida también para choques bidimensionales. En este tipo de choques las velocidades inicial y final no están en una sola recta. Las cantidades iniciales de movimiento de las partículas en la colisión se pueden descomponer en dos componentes mutuamente perpendiculares, y Los componentes totales x e y deben satisfacer por separado la condición de conservación.
El momento neto antes y después de cualquier choque permanece inalterable, inclusive cuando los objetos que chocan se muevan con ciertos ángulos entre ellos. Para expresar el momento neto al considerar diferentes direcciones, se requiere una técnica denominada adición vectorial.
El momento de cada objeto se expresa como un vector; el momento neto se encuentra combinando los vectores en forma geométrica. Una bomba que durante su caída explota en dos fragmentos. Los valores de momento de los fragmentos se combinan por adición vectorial para igualar el momento original de la bomba en caída.
Se pueden aplicar los argumentos de la conservación de la cantidad de movimiento a situaciones en las cuales no es cero, pero uno o dos de sus componentes sí. En estos casos, se conservan los componentes correspondientes de . El problema de un proyectil que explota en vuelo es un ejemplo en el cual se puede seguir este camino. La fuerza sobre el sistema no es cero, porque el sistema está sujeto a la gravedad. Sin embargo, esta fuerza no tiene componentes horizontales, y por tanto se conservan los componentes horizontales de . Se presentan estos casos más complicados no como un tema de estudio más profundo sino para conocer situaciones más generales y apreciar que aun cuando la idea de la conservación del momento es elegantemente simple, su aplicación a choques más complicados puede ser difícil especialmente si no se domina la adición vectorial.
Cualquiera que sea la naturaleza de un choque o por muy complicado que se presente, el momento total antes, durante y después de él se mantiene inalterable. Este concepto extremadamente útil permite aprender mucho de los choques haciendo caso omiso de la forma de las fuerzas que interactúan en ellos.
Centro de masas
Suponga que tiene dos bloques de masas m1 y m2 que están unidos por medio de un resorte comprimido. Si dichas masas son dejadas libres y se supone que no hay roce, el cuerpo de masa m1adquiere una velocidad y el cuerpo de masa m2 adquiere una velocidad , quedando luego el resorte en reposo.
La cantidad de movimiento antes de la interacción es nula porque las masas están en reposo. La suma de las cantidades de movimiento después de la interacción será: m1 + m2
Por el principio de la conservación de la cantidad de movimiento, m1 + m2= 0 Luego m1= -m2
Si la acción del resorte es instantánea, las dos masas se mueven distancias x1 y x2 de su posición inicial, con velocidades constantes, dada cada una en módulo por:
= x1 /
= x2/
Sustituyendo (2) en (1) se tiene que m1. x1/ = m2. x2/
Donde m1. x1= m2. x2
luego
Como puede notarse, esta expresión dice que las distancias recorridas por los cuerpos en relación con el punto donde partieron son inversamente proporcionales a las masas. Esto significa que la mayor distancia la recorre el cuerpo de menor masa.
El centro de masas es el punto que divide la distancia que separa los cuerpos en proporción inversa a sus masas.
Expresión matemática del centro de masa de un sistema en relación a un punto de origen.
Considere dos masas m1 y m2, cuyas distancias a un origen 0 , son respectivamente x1 y x2.
Sea c un punto llamado centro de masas del sistema, el cual está a una distancia xcm del origen.
La expresión para la coordenada x del centro de masas es:
Suscribirse a:
Entradas (Atom)